Impressum Datenschutz

Mathematik in der Oberstufe

Lösungen zu den Aufgaben zum Abstand Punkt-Ebene (Lotfußpunktverfahren)

Da ich einige Beispiele im Artikel Abstand Punkt-Ebene: Lotfußpunktverfahren ausführlich vorgerechnet habe, finden Sie hier zu den Standardrechnungen nur einige Zwischenschritte angegeben, aber nicht die vollständige Rechnung.

Ortsvektoren zu Punkten bezeichne ich mit den passenden Kleinbuchstaben, also $\overrightarrow{OA}=\vec a,\overrightarrow{OM}=\vec m$ usw.

  1. Hilfsgerade/Lotgerade: $h:\vec x=\begin{pmatrix}10\\-1\\-4\end{pmatrix}+t\,\begin{pmatrix}2\\-8\\16\end{pmatrix}$
    $h$ in $E: \quad \ldots \quad\ \Rightarrow t=\dfrac 14; F(10{,}5|-3|0)$
    $d=|\overrightarrow{PF}|=\sqrt{0{,}5^2+(-2)^2+4^2}=4{,}5 \text{ LE}$
    1. Die Aufgabenstellung lässt zu, dass Sie die Ebenen auf Identität prüfen, indem Sie die Parametergleichung in die Koordinatengleichung einsetzen:
      $\begin{align*} 2+2r+4s-2(-2+r+2s)&=6\\ 2+2r+4s+4-2r-4s&=6\\ 6&=6 \quad \text{ (wahr)} \end{align*}$
      Damit sind die Ebenen identisch; beide Gleichungen beschreiben dieselbe Ebene.
      Natürlich können Sie auch die Parametergleichung in die Koordinatenform umwandeln.
    2. Ursprung: $h_1:\vec x=t\,\begin{pmatrix}1\\0\\-2\end{pmatrix}; t_1=1{,}2; F_1(1{,}2|0|-2{,}4)$
      $d_1=|\overrightarrow{OF_1}|=\sqrt{1{,}2^2+0^2+(-2{,}4)^2}=\sqrt{7{,}2}\approx 2{,}68\text{ LE}$
      Punkt P: $h_2:\vec x=\begin{pmatrix}10\\2\\-3\end{pmatrix}+t\,\begin{pmatrix}1\\0\\-2\end{pmatrix}; t_2=-2; F_2(8|2|1)$
      $d_2=|\overrightarrow{PF_2}|=\sqrt{(-2)^2+0^2+4^2}=\sqrt{20}\approx 4{,}47\text{ LE}$
    3. Die Parameter $t_1$ und $t_2$ haben verschiedene Vorzeichen. Man durchläuft den Richtungsvektor bzw. Normalenvektor in entgegengesetzte Richtungen, um vom Stützpunkt aus zur Ebene zu gelangen. Dies bedeutet anschaulich, dass die Stützpunkte der beiden Geraden auf verschiedenen „Seiten“ (in verschiedenen Halbräumen) der Ebene liegen müssen.
    1. Am einfachsten machen Sie die Punktprobe:
      $\begin{align*}A:\; 4+2\cdot 3-2\cdot 1&=8\\8&=8\quad \text{ (wahr) } \Rightarrow A\in E\end{align*}$
      Entsprechend gehen Sie für $B,C$ vor. Für $D$ können Sie argumentieren, dass $ABCD$ laut Aufgabenstellung ein Rechteck bildet und der vierte Punkt deshalb nicht außerhalb der Ebene liegen kann.
    2. $h:\vec x=\begin{pmatrix}4\\1\\8\end{pmatrix}+t\,\begin{pmatrix}1\\2\\-2\end{pmatrix}; t=2; F(6|5|4)$
    3. $G=|\overrightarrow{AB}|\cdot |\overrightarrow{AD}|;\; h=|\overrightarrow{SF}|$
      $\overrightarrow{AB}=\begin{pmatrix}4\\6\\4\end{pmatrix}-\begin{pmatrix}4\\3\\1\end{pmatrix}=\begin{pmatrix}0\\3\\3\end{pmatrix}\quad |\overrightarrow{AB}|=\sqrt{0^2+3^2+3^2}=\sqrt{18}\text{ LE}$
      $\overrightarrow{AD}=\begin{pmatrix}12\\1\\3\end{pmatrix}-\begin{pmatrix}4\\3\\1\end{pmatrix}=\begin{pmatrix}8\\-2\\2\end{pmatrix}\quad |\overrightarrow{AD}|=\sqrt{8^2+(-2)^2+2^2}=\sqrt{72}\text{ LE}$
      $\overrightarrow{SF}=\begin{pmatrix}6\\5\\4\end{pmatrix}-\begin{pmatrix}4\\1\\8\end{pmatrix}=\begin{pmatrix}2\\4\\-4\end{pmatrix}\quad |\overrightarrow{SF}|=\sqrt{2^2+4^2+(-4)^2}=6\text{ LE}$
      $V=\tfrac 13 \cdot \sqrt{18}\cdot \sqrt{72}\cdot 6=72\text{ VE}$
    4. Den Mittelpunkt des Rechtecks können Sie mit $\vec m =\vec a+\tfrac 12 \cdot \overrightarrow{AC}$ oder mit der Formel $\vec m=\tfrac 12 \left( \vec a+\vec c\right)$ berechnen. Es ergibt sich $M(8|3{,}5|3{,}5)$.
    5. Aus der Skizze ergibt sich, dass der Vektor $\overrightarrow{SF}$ nur geeignet verschoben werden muss. 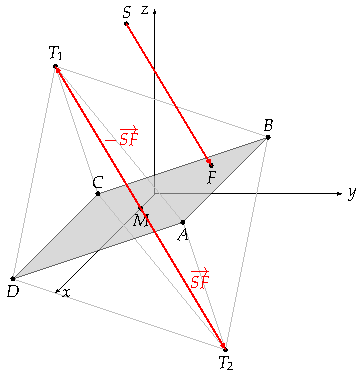Lösung: schiefe Pyramide Mit der hier gewählten Orientierung ergibt sich:
      $\vec t_1=\vec m-\overrightarrow{SF}=\begin{pmatrix}8\\3{,}5\\3{,}5\end{pmatrix}-\begin{pmatrix}2\\4\\-4\end{pmatrix}=\begin{pmatrix}6\\-0{,}5\\7{,}5\end{pmatrix}\Rightarrow T_1(6|-0{,}5|7{,}5)$
      $\vec t_2=\vec m+\overrightarrow{SF}=\begin{pmatrix}8\\3{,}5\\3{,}5\end{pmatrix}+\begin{pmatrix}2\\4\\-4\end{pmatrix}=\begin{pmatrix}10\\7{,}5\\-0{,}5\end{pmatrix}\Rightarrow T_2(10|7{,}5|-0{,}5)$
  4. Da die Punkte $ABCDEFGH$ einen Quader bilden, gilt $F(10|0|3)$.
    1. Die Formulierung „möglichst kurz“ weist darauf hin, dass von $F$ aus das Lot auf die Ebene $E_1$ zu fällen ist.
      $h:\vec x=\begin{pmatrix}10\\0\\3\end{pmatrix}+t\,\begin{pmatrix}0\\1\\3\end{pmatrix}; t=0{,}6; L(10|0{,}6|4{,}8)$
    2. Eine Kantenlänge der Rechtecke kann aus den Koordinaten abgelesen werden.
      $\overrightarrow{FL}=\begin{pmatrix}10\\0{,}6\\4{,}8\end{pmatrix}-\begin{pmatrix}10\\0\\3\end{pmatrix}=\begin{pmatrix}0\\0{,}6\\1{,}8\end{pmatrix}\quad |\overrightarrow{FL}|=\sqrt{0^2+0{,}6^2+1{,}8^2}=\sqrt{3{,}6}\text{ m}$
      $\overrightarrow{GL}=\begin{pmatrix}10\\0{,}6\\4{,}8\end{pmatrix}-\begin{pmatrix}10\\6\\3\end{pmatrix}=\begin{pmatrix}0\\-5{,}4\\1{,}8\end{pmatrix}\quad |\overrightarrow{FL}|=\sqrt{0^2+(-5{,}4)^2+1{,}8^2}=\sqrt{32{,}4}\text{ m}$
      $A_{EFLK}=|\overrightarrow{FE}|\cdot |\overrightarrow{FL}|=10\cdot \sqrt{3{,}6}\approx 18{,}97\text{ m}^2$
      $A_{GHKL}=|\overrightarrow{GH}|\cdot |\overrightarrow{GL}|=10\cdot \sqrt{32{,}4}\approx 56{,}92\text{ m}^2$
      $A_{ges}=A_{EFLK}+ A_{GHKL}\approx 75{,}89\text{ m}^2$

Zurück zu den Aufgaben

Letzte Aktualisierung: 02.12.2015;   © Ina de Brabandt

Teilen Info Bei den "Teilen"-Schaltflächen handelt es sich um rein statische Verlinkungen, d.h. sie senden von sich aus keinerlei Daten an die entsprechenden sozialen Netzwerke. Erst wenn Sie einen Link anklicken, öffnet sich die entsprechende Seite.

↑

Werbung

Abstandsberechnungen im R3

Beispiele, Erklärungen

Aufgaben

Werbung

.