Gegenseitige Lage zweier Geraden

Zwei Geraden in der Ebene können sich schneiden, parallel oder identisch sein. Dies nennt man die (gegenseitige) Lage von Geraden.

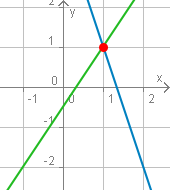
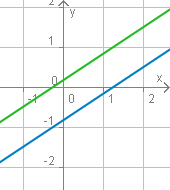
Zwei sich schneidende Geraden Zwei parallele Geraden Zwei identische Geraden

Die Zeichnung lässt bereits vermuten, dass sich zwei Geraden schneiden, wenn ihre Steigungen verschieden sind. Bei gleicher Steigung und unterschiedlichem Achsenabschnitt sind sie parallel; wenn beide Parameter identisch sind, sind auch die Geraden identisch.

Schnittpunkt zweier Geraden

Erstes Beispiel

Gegeben sind die beiden Geraden $f(x)=\frac 12x+\frac 12$ und $g(x)=\frac 13x+\frac 43$.

Wenn sich zwei Geraden schneiden, stimmen im Schnittpunkt $S(\color{#f00}{x_s}|\color{#1a1}{y_s})$ ihre jeweiligen $x$- und $y$-Koordinaten überein. Es müssen also gleichzeitig die Bedingungen $\color{#1a1}{y_s}=\frac 12\color{#f00}{x_s}+\frac 12$ und $\color{#1a1}{y_s}=\frac 13\color{#f00}{x_s}+\frac 43$ erfüllt sein. Aneinandergehängt: $\frac 12 \color{#f00}{x_s}+\frac 12=\color{#1a1}{y_s}=\frac 13\color{#f00}{x_s}+\frac 43$. Es läuft daher darauf hinaus, die Funktionsterme gleichzusetzen. Der Einfachheit halber lässt man den Index „s“ bei $x_s$ üblicherweise weg.

$\begin{align*}f(\color{#f00}{x})&=g(\color{#f00}{x})\\ \tfrac 12\color{#f00}{x}+\tfrac 12&=\tfrac 13\color{#f00}{x}+\tfrac 43&&|-\tfrac 13x-\tfrac 12\\ \tfrac 16\color{#f00}{x}&=\tfrac 56&&|:\left(\tfrac 16\right) \; \text{ bzw. } \; \cdot 6\\\color{#f00}{x}&=\color{#f00}{5}\end{align*}$
Für die zweite Koordinate wird $x=5$ in eine der beiden Funktionsgleichungen eingesetzt:
$f(\color{#f00}{5})=\frac 12 \cdot \color{#f00}{5}+\frac 12=\color{#1a1}{3}$
Die beiden Geraden schneiden sich im Punkt $S(\color{#f00}{5}|\color{#1a1}{3})$. Der Sachverhalt ist in der folgenden Grafik dargestellt.

Schnitt von f(x)=0.5x+0.5 mit g(x)=x/3+4/3

Die gestrichelte graue Gerade entsteht, wenn man bei $g(x)$ die Brüche auf eine Stelle nach dem Komma rundet und somit die Gerade $h(x)=0{,}3x+1{,}3$ betrachtet. Der Schnittpunkt mit $f(x)$ liegt dann bei $T(4|2{,}5)$. Trotz der scheinbar winzigen Abweichung (bei Steigung und Achsenabschnitt jeweils erst die zweite Stelle nach dem Komma) unterscheiden sich die Ergebnisse recht deutlich. Rechnen Sie also unbedingt mit Brüchen – auch der einfachste Schultaschenrechner verfügt heutzutage über eine Bruchtaste, sodass die Ausrede „Ich kann keine Bruchrechnung“ nicht zählt.

Zweites Beispiel

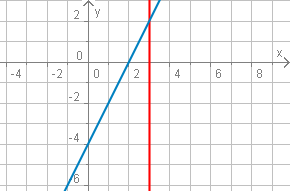y=2x-4 und x=3 (Geraden mit Schnittpunkt, eine achsenparallel) Gesucht ist der Schnittpunkt der Geraden $g(x)=2x-4$ und $h\colon x=3$.

Gleichsetzen ist nicht möglich, da die zweite Gerade keine Funktion ist bzw. kein $y$ enthält. Die Lösung ist aber sehr einfach: die $x$-Koordinate ist bereits bekannt, nämlich 3. Die zweite Koordinate erhalten wir durch Einsetzen in $g$:
$y=2\cdot 3-4=2$

Die Geraden schneiden sich im Punkt $S(3|2)$.

Parallele Geraden

y=0,5x+1 und y=0,5x-2 (parallele Geraden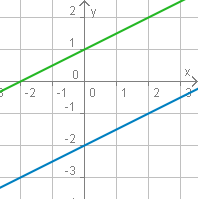) Gegeben sind die Geraden $g(x)=\frac 12x+1$ und $h(x)=\frac 12x-2$. Da die Steigungen gleich und die Achsenabschnitte verschieden sind, sagt uns schon die Anschauung, dass die Geraden parallel verlaufen. Man nennt das auch echt parallel und betont mit dieser Sprechweise, dass die Geraden nicht identisch sind.

Wir wollen jetzt untersuchen, wie sich das in der Rechnung ausdrückt. Wie oben setzen wir dafür die Funktionsterme gleich:

$\begin{align*} \tfrac 12x+1&=\tfrac 12x-2 &&|-\tfrac 12x-1\\0&=-3 && && \text{falsche Aussage}\end{align*}$

Diese Gleichung hat keine Lösung, was sich im Graphen dadurch ausdrückt, dass die Geraden keinen gemeinsamen Punkt haben.

Identische Geraden

y=2/3x-1 und y=2/3x-1 (identische Geraden) Gegeben sind die Geraden $g(x)=\frac 23x-1$ und $h(x)=\frac 23x-1$. Da sowohl die Steigungen als auch die die Achsenabschnitte übereinstimmen, ist anschaulich klar, dass die Geraden identisch sind bzw. übereinander liegen.

Auch hier wollen wir untersuchen, was dabei in der Rechnung geschieht. Wir setzen die Funktionsterme gleich:

$\begin{align*} \tfrac 23x-1&=\tfrac 23x-1&&|-\tfrac 23x+1\\0&=0 && && \text{wahre Aussage}\end{align*}$

Die Gleichung ist für jedes $x\in \mathbb R$ erfüllt. Sie hat also unendlich viele Lösungen, was sich im Graphen dadurch ausdrückt, dass jeder Punkt der Geraden gemeinsamer Punkt ist. Anders ausgedrückt: jeder Punkt der einen Geraden ist auch Punkt der anderen Geraden.

Gerade nicht in Mormalform

Bisher waren die Geraden in Normalform gegeben. Wie geht man vor, wenn das nicht der Fall ist?

Wenn Sie die Geraden nicht nur auf ihre Lage untersuchen, sondern auch zeichnen sollen, wandeln Sie die Geraden erst in die Normalform (Hauptform) um (für die Zeichnung sinnvoll) und können gleichsetzen.
Wenn Sie die Geraden nur rechnerisch auf ihre Lage untersuchen sollen, sind folgende Lösungswege sinnvoll:
- Wenn eine Gleichung nach einer Unbekannten aufgelöst ist, verwenden Sie das Einsetzungsverfahren.
- Wenn keine Gleichung nach einer Unbekannten aufgelöst ist, verwenden Sie das Additionsverfahren.

Prinzipiell können Sie auch in den letzten beiden Fällen in die Normalform umformen, aber das bedeutet mehr Arbeit.

Zusammenfassung

Die Geraden	Das Gleichungssystem hat	Parameter
schneiden sich in einem Punkt.	genau eine Lösung.	$m_1\not =m_2$
sind (echt) parallel bzw. haben keinen Punkt gemeinsam.	keine Lösung.	$m_1=m_2$; $b_1\not= b_2$
sind identisch bzw. haben unendlich viele Punkte gemeinsam (jeden Punkt der Geraden).	unendlich viele Lösungen.	$m_1=m_2$; $b_1=b_2$

Die letzte Spalte gilt natürlich nur für den Fall, dass keine der beteiligten Geraden von der Form $x=a$ ist, also beide von der Gestalt $f_1(x)=m_1x+b_1$ und $f_2(x)=m_2x+b_2$ sind.

Übungsaufgaben

Teilen Info Bei den "Teilen"-Schaltflächen handelt es sich um rein statische Verlinkungen, d.h. sie senden von sich aus keinerlei Daten an die entsprechenden sozialen Netzwerke. Erst wenn Sie einen Link anklicken, öffnet sich die entsprechende Seite.

↑