Abbildungsmatrizen für Abbildungen der Ebene
Mit Matrizen kann man verschiedene mathematische Probleme beschreiben. Die Beschreibung von Gleichungssystemen mithilfe von Matrizen sollten Sie bereits kennen.
Ein bisher in der Schule eher selten behandeltes Thema sind die Abbildungen der Ebene und des Raumes. Darunter versteht man zum Beispiel Drehungen, Verschiebungen und Spiegelungen, die in der Mittelstufe rein zeichnerisch in der Ebene untersucht werden. Diese Abbildungen kann man natürlich auch rechnerisch darstellen, und zwar nicht nur in der Ebene, sondern auch im Raum. Geeignetes Mittel dafür sind Matrizen.
Wir werden uns hier nur lineare Abbildungen ansehen. Diese müssen die Bedingungen $f(x + y) = f(x) + f(y)$ und $f(k\cdot x) = k\cdot f(x)$ ($k$ eine festbleibende reelle Zahl, also eine Konstante) erfüllen. Bei linearen Abbildungen bleibt insbesondere immer der Ursprung fest; es gibt also keine Verschiebungen. Ich beschränke mich auf die bekanntesten Abbildungen in der Schulmathematik: Spiegelungen, Drehungen und Projektionen.
Dieser Artikel ist eher als Wiederholung gedacht, weniger als erste Einführung in das Thema.
Spiegelung an einer Koordinatenachse
Wir schauen uns zunächst eine sehr einfache Abbildung an, nämlich die Spiegelung an der $x$-Achse. Wenn man einen Punkt $P(x|y)$ spiegelt, bleibt die $x$-Koordinate wie sie ist, und bei der $y$-Koordinate dreht sich das Vorzeichen um.
Bildpunkte bezeichnet man üblicherweise mit $P'$, die Koordinaten entsprechend mit $x'$ und $y'$. Für die Spiegelung an der $x$-Achse gilt somit:
$\begin{align}x' &= x\\ y' &= -y\end{align}$
Diese Gleichungen bezeichnet man als Abbildungsgleichungen. Sie stellen die Beziehung zwischen den ursprünglichen Koordinaten und den Bildkoordinaten her, genauer: sie geben an, wie man die Koordinaten des Bildpunktes aus den Koordinaten des Urbildpunktes berechnet.
Die Abbildungsgleichungen sollen nun mit Hilfe einer Matrix dargestellt werden. Dazu schreiben wir zunächst etwas ausführlicher:
$\begin{align}x' &= 1\cdot x +0\cdot y\\ y' &= 0\cdot x -1\cdot y\end{align}$
Diese Gleichungen kann man in Matrixform schreiben:
$\begin{pmatrix} x'\\y'\end{pmatrix} = \begin{pmatrix} 1 & 0\\0 & -1\end{pmatrix} \cdot \begin{pmatrix} x\\y\end{pmatrix}$ oder $\vec x'= A\cdot \vec x$ mit $A=\begin{pmatrix} 1 & 0\\0 & -1\end{pmatrix}$. Die Schreibweise inklusive des Vektors $\vec x$ heißt weiterhin Abbildungsgleichung, die Matrix A Abbildungsmatrix.
Spiegelung am Koordinatenursprung
Bei der Punktspiegelung am Ursprung drehen sich die Vorzeichen beider Koordinaten um:
$\begin{matrix} x'&=& -x &=& -1\cdot x &+& 0\cdot y\\y'&=& -y &=& 0\cdot x &-&1\cdot y\end{matrix}$
Die Abbildungsmatrix der Punktspiegelung am Ursprung hat damit die Gestalt $A=\begin{pmatrix} -1 & 0\\0 & -1\end{pmatrix}$.
Projektion auf eine Koordinatenachse
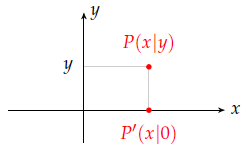Eine weitere einfache Abbildung ist die Projektion auf eine Koordinatenachse, in diesem Beispiel auf die $x$-Achse. Die Abbildungsgleichungen lauten:
$\begin{matrix} x'&=& x &=& 1\cdot x &+& 0\cdot y\\y'&=& 0 &=& 0\cdot x &+&0\cdot y\end{matrix}$
Die Abbildungsmatrix bei Projektion auf die $x$-Achse lautet also $A=\begin{pmatrix} 1 & 0\\0 & 0\end{pmatrix}$.
Drehung um den Ursprung
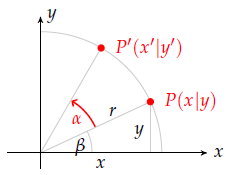Drehungen erfolgen in der Mathematik immer gegen den Uhrzeigersinn. Zur Bestimmung der Abbildungsmatrix ist hier etwas mehr Arbeit erforderlich.
Dafür stellen wir die Koordinaten zunächst anders dar. Da die Seiten $x$, $y$ und $r$ ein rechtwinkliges Dreieck bilden, gilt $\dfrac{x}{r} = \cos(\beta)$ und $\dfrac{y}{r} = \sin(\beta)$. Damit ist
$x = r\cdot \cos(\beta) \qquad y = r\cdot \sin(\beta)$
Für die Koordinaten des Bildpunktes gilt ebenso
$x' = r\cdot \cos(\beta+\alpha) \qquad y' = r\cdot \sin(\beta+\alpha)$
Um $x'$ und $y'$ mithilfe von $x$ und $y$ ausdrücken zu können, benötigen wir die Additionstheoreme:
$\cos(\beta + \alpha) = \cos(\beta)\cdot \cos(\alpha) - \sin(\beta)\cdot \sin(\alpha)$
$\sin(\beta + \alpha) = \sin(\beta)\cdot \cos(\alpha) + \cos(\beta)\cdot \sin(\alpha)$
Damit gilt dann
$\begin{array}{lcccc}x'&=& \underbrace{r\cos(\beta)}_{x}\cdot \cos(\alpha) - \underbrace{r\sin(\beta)}_{y}\cdot \sin(\alpha)&=&x\cdot \cos(\alpha) - y\cdot \sin(\alpha)\\ y'&=& \underbrace{r\sin(\beta)}_{y}\cdot \cos(\alpha) + \underbrace{r\cos(\beta)}_{x}\cdot \sin(\alpha)&=&y\cdot \cos(\alpha) + x\cdot \sin(\alpha)\\\end{array}$
bzw. in der „richtigen“ Reihenfolge:
$\begin{array}{lcc}x'&=& \cos(\alpha) \cdot x- \sin(\alpha) \cdot y\\ y'&=& \sin(\alpha) \cdot x+\cos(\alpha)\cdot y\\\end{array}$
Die Drehmatrix hat somit die Gestalt $A=\begin{pmatrix}\cos(\alpha) & - \sin(\alpha)\\ \sin(\alpha) & \cos(\alpha) \end{pmatrix}$.
Eine Drehung um den Ursprung um den Winkel 180° ist in der Ebene gleichbedeutend mit der Punktspiegelung am Ursprung.
Projektion auf eine beliebige Ursprungsgerade
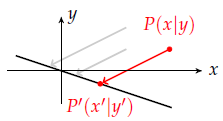Die oben vorgeführte Projektion auf die $x$-Achse war senkrecht (orthogonal), aber das ist nicht notwendig. Bei der häufigsten Anwendung in der Schule, dem Schattenwurf, ist das sogar eher die Ausnahme. Dabei wird in eine vorgegebene Richtung auf eine Gerade projiziert. Weil die Strahlen alle parallel verlaufen, nennt man diese Projektion Parallelprojektion.
Die Abbildungsmatrix der Projektion wird in der Schule üblicherweise nicht allgemein angegeben, sondern immer nur für eine spezielle Projektionsgerade und eine spezielle Projektionsrichtung ermittelt. In unserem Beispiel soll ein Punkt $P(x|y)$ in Richtung des Vektors $\begin{pmatrix}2\\1\end{pmatrix}$ auf die Gerade $p: x + 3y = 0$ projiziert werden. Der Punkt $P(x|y)$ muss dennoch die allgemeinen unbekannten Koordinaten behalten, da man für die Berechnung der Abbildungsmatrix die Abbildungsgleichungen in der Form $x' = \text{Zahl} \cdot x + \text{Zahl} \cdot y$ bzw. $y' = \text{Zahl} \cdot x + \text{Zahl} \cdot y$ benötigt.
Der Bildpunkt $P'$ ist der Schnittpunkt der Projektionsgeraden mit der Geraden durch $P$ in Richtung des vorgegebenen Vektors, also mit $g\colon \vec x' = \begin{pmatrix} x\\y \end{pmatrix} + t\cdot \begin{pmatrix}2\\1\end{pmatrix}$. Um den Schnittpunkt zu berechnen, wird $g$ in die Projektionsgerade $p$ eingesetzt:
$\begin{array}{rcll}x+2t+3\cdot(y + t) &=& 0\\ x+2t+3y + 3t &=& 0&|-x-3y\\ 5t &=& -x - 3y&| :5\\ t &=& -0{,}2x - 0{,}6y\end{array}$
Setzt man $t$ in die Gerade $g$ ein, so erhält man als Ortsvektor des Schnittpunktes
$\begin{align*}\begin{pmatrix}x'\\y' \end{pmatrix} &\,=\begin{pmatrix}x\\y\end{pmatrix}+(-0{,}2x - 0{,}6y)\cdot \begin{pmatrix}2\\1 \end{pmatrix}\\ &\,=\begin{pmatrix}x\\y\end{pmatrix}+ \begin{pmatrix}-0{,}4x - 1{,}2y\\-0{,}2x - 0{,}6y \end{pmatrix}\\ &\,=\begin{pmatrix}0{,}6x - 1{,}2y\\-0{,}2x + 0{,}4y \end{pmatrix}\end{align*}$
und daraus wiederum die Abbildungsmatrix $A=\begin{pmatrix}0{,}6 &- 1{,}2\\-0{,}2 & 0{,}4 \end{pmatrix}$.
Die Projektion verlief hier längs einer vorgegebenen Richtung. Soll orthogonal projiziert werden, so liest man aus der Projektionsgeraden den Normalenvektor $\vec n =\begin{pmatrix}1\\3\end{pmatrix}$ ab und führt die Rechnung entsprechend durch. Als Abbildungsmatrix erhält man in diesem Fall $A=\begin{pmatrix}0{,}9 &- 0{,}3\\-0{,}3 & 0{,}1 \end{pmatrix}$.
Vielleicht fragen Sie sich, ob man auch von einem Punkt aus projizieren kann, zum Beispiel bei einer punktförmigen Lichtquelle. Ja, prinzipiell ist es möglich, wenn es auch nicht zu jedem Punkt einen Bildpunkt gibt. Da man von einem Zentrum aus projiziert, nennt man sie Zentralprojektion. Die Abbildung ist allerdings nicht linear und kann daher nicht durch eine Matrix beschrieben werden.
Spiegelung an einer beliebigen Ursprungsgeraden
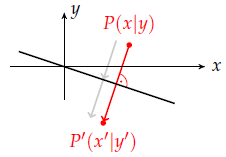Die Spiegelung wird in der Schule immer orthogonal (rechtwinklig) zur Spiegelachse durchgeführt. Die Zeichnung lässt bereits ahnen, dass man ähnlich wie bei der Projektion vorgeht: man berechnet zunächst den Schnittpunkt mit der Geraden. Da man jetzt den Weg vom Urbildpunkt $P$ zur Geraden zweimal laufen muss, um den Bildpunkt $P'$ zu erhalten, verdoppelt man einfach den Parameter aus der Geradengleichung.
Auch die Abbildungsmatrix einer Spiegelung wird nicht allgemein berechnet, sondern nur für ein konkretes Beispiel. Der Punkt $P(x|y)$ soll an der Geraden bzw. Achse $p\colon x + 3y = 0$ gespiegelt werden. Zunächst wird wieder die Gerade aufgestellt. Da die Hilfsgerade diesmal senkrecht auf der Achse stehen soll, verwendet man als Richtungsvektor den Normalenvektor $\vec n = \begin{pmatrix}1\\3\end{pmatrix}$ und muss somit den Schnittpunkt von $p\colon x + 3y = 0 $ mit $g\colon \vec x' = \begin{pmatrix} x\\y \end{pmatrix} + t\cdot \begin{pmatrix}1\\3\end{pmatrix}$ berechnen:
$\begin{array}{rcll}x+t+3\cdot(y + 3t) &=& 0\\ x+t+3y + 9t &=& 0&|-x-3y\\ 10t &=& -x - 3y&| :10\\ t &=& -0{,}1x - 0{,}3y\end{array}$
Es ist nicht nötig, den Schnittpunkt zu berechnen, der ja nur ein Hilfspunkt ist. Stattdessen verdoppelt man den Parameter $t$ und erhält sofort die Koordinaten des Bildpunktes
$\begin{align*}\begin{pmatrix}x'\\y' \end{pmatrix} &\,=\begin{pmatrix}x\\y\end{pmatrix}+2\cdot (-0{,}1x - 0{,}3y)\cdot \begin{pmatrix}1\\3 \end{pmatrix}\\ &\,=\begin{pmatrix}x\\y\end{pmatrix}+ \begin{pmatrix}-0{,}2x - 0{,}6y\\-0{,}6x - 1{,}8y \end{pmatrix}\\ &\,= \begin{pmatrix}0{,}8x - 0{,}6y\\-0{,}6x - 0{,}8y \end{pmatrix}\end{align*}$
und daraus wiederum die Abbildungsmatrix $A=\begin{pmatrix}0{,}8 & - 0{,}6\\-0{,}6 & - 0{,}8 \end{pmatrix}$.
Schrägspiegelung
Auch wenn es in der Schule eher selten vorkommt, möchte ich Ihnen noch kurz die Schrägspiegelung vorstellen. Wie der Name schon sagt, wird dabei nicht orthogonal, sondern schräg zur Achse gespiegelt.
Die Bestimmung der Abbildungsmatrix sollte nun kein Problem mehr für Sie darstellen. Wenn Sie an der Geraden $p\colon x + 3y = 0$ in Richtung des Vektors $\begin{pmatrix}2\\1 \end{pmatrix}$ spiegeln, ergibt sich als Abbildungsmatrix $A=\begin{pmatrix}0{,}2 &- 2{,}4\\-0{,}4 &- 0{,}2 \end{pmatrix}$.
Und warum immer der Ursprung?
Drehung um den Ursprung, Spiegelung an oder Projektion auf eine Ursprungsgerade – die Einschränkung ist für diesen Artikel notwendig, weil ich nur lineare Abbildungen beschrieben habe, und diese müssen den Ursprung festlassen. Spiegelt man dagegen an einer Geraden, die nicht durch den Ursprung geht, so würde der Ursprung auf einen anderen Punkt abgebildet. Das gilt auch für alle anderen hier vorgestellten Abbildungen.
Letzte Aktualisierung: 02.12.2015; © Ina de Brabandt
Werbung